Atendiendo a una petición, y aunque sea con algo de retraso,
voy a tratar algunos aspectos relativos a los eclipses
Sin duda los eclipses son los
fenómenos astronómicos más relevantes sobre todo de cara al gran público.
Hace un par de meses ocurrieron dos
eclipses, el 14 de octubre de sol y el 28 de Luna
Alguien me dijo que parecía
una casualidad, dos tan seguidos, aunque lo cierto es que siempre ocurre algo
parecido. Precisamente los próximos serán el 25 de marzo, penumbral de luna, y el 8 de abril, total de sol. Pero podrían haber sido tres.
Como en la mayoría de las
relaciones humanas, los eclipses normalmente van por parejas pero de vez en
cuando también aparecen los tríos. Dos de luna escoltando a uno de sol o al
revés, todos ellos separados por 14 o 15 días.
Veamos las razones, empezando por
el principio:
Si la órbita en que la Tierra
gira alrededor del Sol (la eclíptica) y la de la Luna alrededor de la Tierra
estuvieran en el mismo plano, en todas las lunas llenas y nuevas habría eclipse:
Pero entre ambos planos orbitales
hay una inclinación de poco más de 5º, y los puntos en que se cortan (en los
que la Luna se ve en la eclíptica) se llaman nodos. La Luna estará en el nodo
ascendente (que se representa por la letra omega) cuando pasa del sur al norte
de la Eclíptica, y el descendente (una omega invertida) el contrario.
Para que se produzca un eclipse
la Luna debe estar cerca de uno de los nodos y así se interponga en la
dirección del Sol (eclipse de Sol) o entre en la sombra de la Tierra (eclipse
de Luna). Además, tal como se ha dicho, deberá ser luna llena o nueva para que
los 3 astros estén alineados
Tanto en A como en B se han
representado las dos posiciones de la luna en llena y nueva. En A no hay
eclipse porque aunque están alineados los tres astros, la Luna no está en la
eclíptica y las sombras pasan por debajo del otro astro. En B hay eclipses.
Después de un eclipse en que la sombra pase exactamente por el nodo, debido a
la traslación de la Tierra, en cada lunación la línea Sol-Tierra-Luna (o Sol-Luna-Tierra) va
apuntando a lugares diferentes y se va alejando del nodo (cada media lunación
va retrasando el paso por el nodo) de manera que no se producirá un
nuevo eclipse, aunque el nodo también se desplaza pero mucho menos:
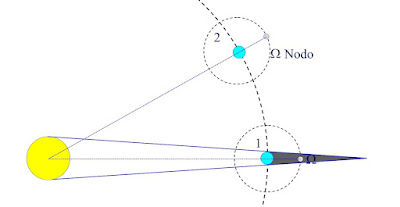 |
| En 1 hay eclipse de luna al coincidir la luna llena con el paso por el nodo (en este caso el ascendente). En la siguiente lunación en 2 no hay eclipse porque la Luna no está en el nodo y la sombra de la Tierra pasará por encima de ella. |
Si la Luna nueva está exactamente
en el nodo se producirá un eclipse total o anular de sol, y si la luna llena
está en el nodo (o muy cerca de él) se producirá un eclipse total de Luna. Pero
no es necesario que esté exactamente en el nodo para que ocurra un eclipse, y
considerando también los parciales y penumbrales, es suficiente que la Luna (nueva o llena) esté a una
distancia al nodo menor de 16.4º en los
de sol y 15.7º en los de luna, tal como se calcula en el anexo. Estos números pueden variar ligeramente según las distancias entre los 3 astros ese día, de manera que estos números son los valores medios.
Por ejemplo, el siguiente gráfico representa la situación
del último eclipse de Luna, del 28 de octubre de 2023, donde la distancia de la Luna (en
el momento del máximo del eclipse) al nodo es de 14.52º después de pasar por él. Al ser menor que 15.7º se produjo el eclipse, pero al no estar muy cerca del nodo fue bastante pobre.
Si la distancia de la Luna al nodo durante el eclipse hubiera sido menor, como en el siguiente caso, la parte eclipsada de la Luna lógicamente habría sido mayor.
Estas imágenes planas son la
representación de una porción de la esfera celeste, por lo que la distancia del
nodo al centro de la sombra de la Tierra es un ángulo y se expresa en grados, siendo
prácticamente igual a la distancia del nodo a la posición de la Luna.
Como se ha dicho, la clave está
en que los eclipses ocurren necesariamente en luna nueva o llena, y cerca de
los nodos de la órbita lunar, con los márgenes indicados antes. Tal como se
representa en el siguiente gráfico, si ocurre un eclipse antes del nodo (por
ejemplo de Sol y luna nueva en la posición 1) al cabo de media lunación
ocurrirá otro (en luna llena -2-) después de pasar la Luna por
el otro nodo.
Debido a que la Tierra se ha
desplazado en esas 2 semanas en su movimiento de traslación, la posición
relativa respecto al nodo de la luna llena o nueva no será la misma y en
la mayoría de los casos en la siguiente ocasión ya se habrá alejado y no habrá
eclipse. Como se verá luego, también influye en menor medida el ligero
desplazamiento de los nodos.
Pero en ocasiones hay margen para
que ocurran 3 eclipses también separados por 2 semanas del primero al segundo y
del segundo al tercero: de Luna-Sol-Luna como en el siguiente gráfico, o de
Sol-Luna-Sol.
En este caso el primero (1)
ocurrirá con la Luna relativamente alejada del nodo, aunque dentro del margen
indicado, el segundo (2) muy cerca del nodo con lo que será un eclipse muy
bueno, y el tercero (3) con la Luna alejada también del nodo.
Esta situación, vista desde la
Tierra, se representa en el siguiente gráfico, donde se ha desplegado toda la
línea de la eclíptica en una recta:
Se ha situado el primer eclipse
(a la derecha) justo en el borde del margen para ver la situación más favorable
para que ocurran más eclipses. Aún así, y aunque se producen 3 eclipses, el
tercero está casi en el otro borde, por lo que es extremadamente difícil que en
las situaciones medias, ocurran 3 seguidos: A poco que el 1 se acerque al nodo,
el 3 se saldría del margen.
Para mayor detalle repito el mismo gráfico con más parámetros que, aunque puedan hacerlo más engorroso, justifican mejor el resultado.
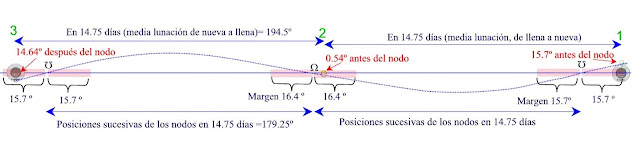 |
| Al igual que en el gráfico anterior y el siguiente, todo está a escala |
Por tanto, cabe justo justo un trío
comenzando y acabando con eclipses penumbrales mínimos (en el borde de los
márgenes), pero sería mucha casualidad.
Una pareja siempre entrará, porque
el primer eclipse (1) siempre estará en el margen previo al nodo (antes de él, porque si estuviera después del nodo habría ocurrido otro eclipse antes),
con lo que media lunación después (en 2) también habrá eclipse porque estará
también en la zona dentro del margen del siguiente nodo, pero si el
primer eclipse no ocurre al principio del margen como antes, en 3 ya se saldrá
y no habrá más, como se aprecia en este otro gráfico:
En este caso se producen solo dos eclipses seguidos, que es
lo más habitual.
Todo esto se obtiene redondeando y utilizando
valores medios de los parámetros, pero que varían ligeramente según las posiciones de la Tierra y
la Luna en sus órbitas. En el anexo se calculan los diferentes parámetros y se
recogen en los gráficos.
¿Hay muchos tríos?
Tal como puede deducirse de la
anterior explicación y los gráficos, no son muchos.
Concretamente entre 1950 y 2050
ocurren 22 tríos frente a 184 parejas. Los tríos son 10 de Sol-Luna-Sol y 12 de
Luna-Sol-Luna.
El último fue en 2020 y el próximo será en 2029, ambos en junio y julio. De todas formas no hay que decir la frase de "¡Todavía faltan más de 5 años!" porque una pareja es más interesante que un trío, ya que los de los extremos de éste son eclipses muy pequeños (los de sol solo parciales y visibles desde latitudes muy altas, y los de luna solo penumbrales)
Por ejemplo, desde la mayor parte de la península Ibérica se verá un extraordinario eclipse de sol total y un eclipse de luna casi total en agosto de 2026. ¡Ya queda menos!
Es muy curioso constatar que todos
los tríos de este periodo ocurren en la misma época del año:
De los 22 citados, 9 fueron en junio-julio, 7 en
julio-agosto, 3 en agosto-septiembre y 2 en mayo-junio y 1 en abril-mayo
Claramente prevalece las
cercanías a julio y en esos 100 años no ocurre nunca en invierno ni en otoño.
Esto es porque en el afelio (principios de julio) la Tierra se mueve más despacio y por ello la lunación es
más corta (como se explica en el anexo de este artículo). Con ello se acortarían
los intervalos entre las lunas nuevas y llenas, y como se deduce de los
gráficos anteriores entrarían más fácilmente dentro de los márgenes. En los
meses próximos a enero ocurre lo contrario: al pasar la Tierra por el perihelio
las lunaciones son más largas, la distancia entre la posición 1 y 3 de los gráficos anteriores será más grande y será difícil (aunque no imposible) que ambas queden incluidas en los
márgenes con lo que normalmente no habrá tríos.
En este anexo aparece mucha geometría y trigonometría, para deducir el tamaño de los márgenes de los eclipses. Si no te gustan esas cosas, te aconsejo que no lo mires.
Vamos a obtener los diferentes
parámetros numéricos que se han utilizado en la explicación, concretamente los
márgenes en torno al nodo, dentro de los cuales se producen los eclipses.
- En los eclipses penumbrales de Luna: (su margen será el máximo incluyendo todos los tipos de eclipses lunares)
a) Cálculo previo. Gráfico en alzado, con la eclíptica de perfil.
Como el cono de penumbra está determinado por las rectas que tocan el Sol y la Tierra cruzándose entre los dos astros, se calcula primero la distancia del borde del cono, a la Tierra (Y). Se utilizan como datos la distancia media del Sol a la Tierra y el radio de los dos astros, utilizando triángulos semejantes.
b) Se calcula la distancia máxima de la Luna al eje del cono de la sombra para que se produzca un eclipse penumbral (Z), y luego el ángulo desde la Tierra del eje del cono al centro de la Luna. Se traza desde el centro de la Tierra porque el gráfico no está a escala y el tamaño a escala de nuestro planeta sería mínimo. (z)
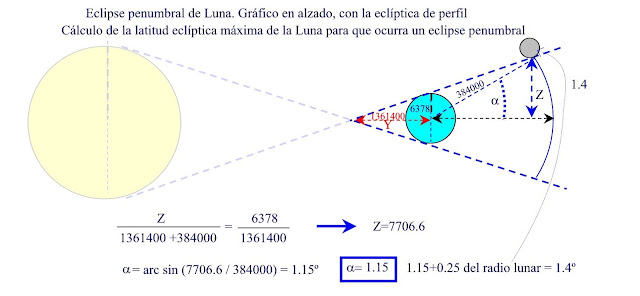
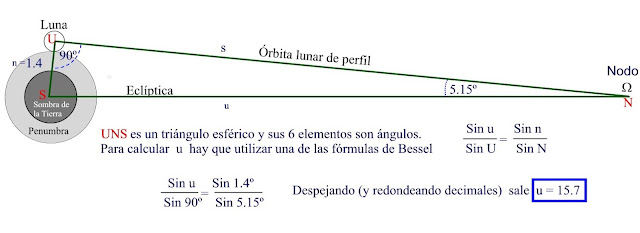
c) El siguiente gráfico está en un plano perpendicular al anterior, delante de él. Está en alzado, con la eclíptica horizontal. Se calcula la separación máxima u de la Luna respecto al nodo, se le llama n al valor obtenido de alfa, y está a escala.
- En los eclipses de Sol
Tal como se representa en el siguiente gráfico, en principio para que haya
eclipse la distancia angular entre el centro del Sol y el de la Luna debería ser menor de 0.5º porque cada uno de ellos tiene un radio aparente de 0.25º. Pero desde cada lugar de la Tierra se ve la Luna en diferente
posición por el paralaje, y los eclipses de Sol no se ven igual desde
diferentes lugares. Desde una posición media la Luna puede verse a 0.95º desde
un extremo, tal como se calcula.
Así al sumar 0.95º + 0.5º queda 1.45º a
los que estaría la Luna separada del Sol como máximo para que se produzca el
eclipse.
Si buscas estos datos en internet, es probable que encuentres valores diferentes. Eso es porque aquí se han tomado valores medios y en el caso de los eclipses de luna en ocasiones se no se consideran los penumbrales.
Eclipse parcial.
a) Si queremos obtener el margen para un eclipse parcial, habrá que empezar calculando la longitud del cono de sombra de la Tierra (Z), que en promedio, será:
b) Distancia máxima de la Luna al eje del cono de la sombra para que se produzca un eclipse parcial (La Luna tocará el cono de sombra, o mejor dicho lo intersectará muy levemente)
c) Ángulo desde la Tierra del eje del cono al centro de la Luna. Se traza desde el centro de la Tierra porque el gráfico no está a escala y el tamaño a escala de nuestro planeta sería mínimo. Se toma el centro de la Luna porque es la referencia que se utiliza para determinar su situación:
d) Finalmente en un triángulo esférico situado en un plano perpendicular a los anteriores se calcula el margen N:
10.5º es el margen medio para un eclipse parcial. Si queremos calcular el margen máximo, que es lo que suele aparecer, el cálculo será igual pero con la Tierra en el afelio (distancia al Sol 152100000 km) y la Luna en el perigeo (a una distancia de 356600 k)
Margen máximo de un eclipse parcial
Se obtiene exactamente igual que en el cálculo anterior pero tomando la posición de la Tierra en el afelio (Distancia Tierra-Sol= 152000000 km) y la Luna en el perigeo (Distancia Tierra-Luna = 356595):
Este es el valor que se suele encontrar: "Un eclipse lunar parcial solo puede ocurrir cuando la luna está a menos de 11.4º de uno de los nodos"
Pero cuidado, que esta condición es necesaria pero no suficiente.
Eclipse total de Luna
Los cálculos serían igual que los anteriores, pero en el apartado c) en vez de sumar el radio lunar (0.25º) habría que restarlo porque toda la Luna debe quedar dentro del cono de sombra.





















.jpg)



.gif)


























